[ad_1]
How to calculate sample size
For the purpose of estimating prevalence, the sample size formula is fairly simple and available in many books.
the following formula [2] will be used:
$$n=\frac{{Z}^{2}P\left(1-P\right)}{{d}^{2}}$$
Where n= sample size,
Z.= Z-statistic for confidence level (1.96 at 95% confidence level),
P.= expected prevalence or rate, and .
d= precision.
However, we do not recommend that researchers use formulas, as manual calculations are subject to human error. Using the available software, you can concentrate on carefully choosing the right parameters for your calculations.
Appropriate selection of parameters
The formula above shows the three parameters to be determined.
Parameter 1: Confidence
If you took a sample but want to know about the population from which the sample was taken (such as smoking prevalence), you don’t know the exact smoking prevalence of the population because you didn’t study every member of the population . However, a sample survey provides an estimate with lower and upper bounds (informally the ‘range’, but statistically called the ‘interval’) of population prevalence. We usually compute these lower and upper bounds, or intervals of some level of confidence. A commonly used or almost always used “confidence level” for these intervals or estimates is 95% (called the 95% confidence interval, CI) in the medical and health field. Additionally, most data analysis software provides 95% CI results by default. For these reasons, and to minimize user error by non-statisticians, we fixed the confidence level at 95% without giving the user a choice in these presented calculators.
Parameter 2: Accuracy
As mentioned above, we do not study all members of the population, so we do not know the exact prevalence in the population. Therefore, the prevalence calculated from the sample can deviate (error) from the prevalence of the population. This deviation is called sampling error. We also know that the larger the sample size, the smaller the estimation error. Error is calculated as precision, also known as “margin of error”.
In practice, precision reflects the width of the 95% confidence interval. If we decide to choose an absolute precision of ± 2% when estimating the prevalence, we should expect the resulting 95% CI width to be 4% (e.g. 95% CI: 23%, 27%). If the absolute precision in estimating prevalence is ± 5%, then the result should be expected to have a 95% CI range of 10% (e.g. 95% CI: 20%, 30%) . The CI width is twice the precision. Details are shown in Table 1.
This is an opportunity for the researcher to decide the precision (margin of error) and width of the CIs they wish to see in their results. Typically, researchers want her CI to be narrow, but narrower widths are more expensive (larger sample size). Even if the researcher chooses a smaller sample size, the researcher can also predict or assess how poor her CI width of the outcome will be. Therefore, this is a well-informed decision to be made by researchers.
In practice, here are some recommendations for choosing accuracy values (Table 2). In general, well-funded or large studies aimed at attracting the attention of policy makers should aim for 2-3% accuracy. A 4-5% accuracy can be considered in the project. Due to limited resources, a researcher should consider the study a preliminary study if the accuracy is above his 5% (say 10%).
However, the above recommendations apply when the expected prevalence is 10-90%. If the expected prevalence is too small (less than 10%) or too large (more than 90%), a much smaller precision should be applied. It’s clear that 5% accuracy is possible for a 50% predicted prevalence, but 5% accuracy for a 2% predicted prevalence is completely inappropriate.
We use the example in Table 2 to show the details of the expected prevalence accuracy.
Parameter 3: Data variability
The more variable the data, the larger the sample size required. This relationship can be illustrated with a simple analogy. As you make the soup and near the finish, stir it well before tasting. Stir well and have near zero variation, so you always need a very small amount (small sample size) to taste.
In practice, when estimating prevalence, prevalence affects this variability and thus the required sample size. The relationship between prevalence and sample size is shown in Figure 1.
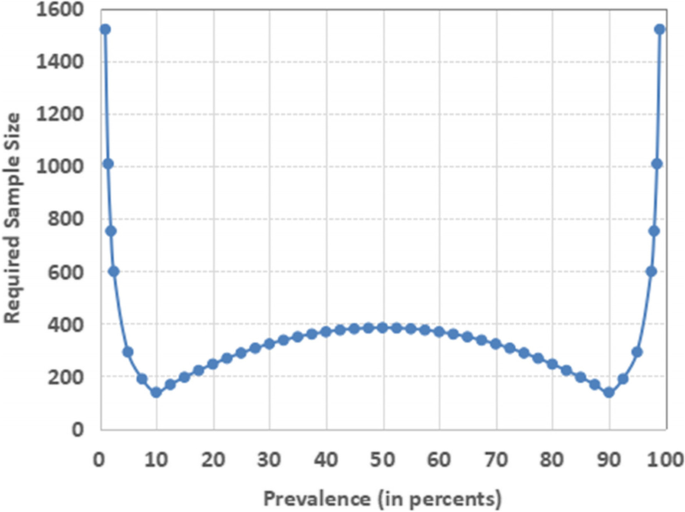
Effect on prevalence and sample size
Obviously, estimating the prevalence is the purpose of the study, and researchers do not know this prevalence. Therefore, to calculate the sample size, we usually find from the most recent published studies using similar study populations. If no suitable studies are found in the literature, we may consider conducting a pilot study.
If you find more than one suitable prevalence from the literature, say in the range 15-30%, 30% is the largest sample size in the prevalence range 15-30%. Similarly, if the prevalence is in the 60-80% range in the recent literature, then 60% should be used because we want the largest sample size in that range.
Note that some books and guidelines suggest using an expected prevalence of 50% when no prevalence could be obtained. [2, 14, 15]We do not recommend this practice. Note in Figure 1 that a prevalence of 50% produces the largest sample size only within the range of 10-90% of prevalence. The required sample size is much larger for areas below 10% and above 90%. So don’t use the 50% prevalence shortcut. It is best to calculate the sample size with an appropriate predicted prevalence. Researchers can find expected prevalence ranges and apply the recommendations in the previous paragraph.
In this figure, we used small-scale study precision to generate Figure 1 (Table 2). It uses a fixed 5% precision for predicted prevalences between 10% and 90%, half the predicted prevalence for predicted prevalences less than 10%, and higher predicted prevalences. Means use half of (100 to predicted prevalence) for prevalence. 90 and above.
Parameter 4: Expected Loss
Loss of sample size always occurs during the research process due to several reasons such as non-response, incomplete data and loss of follow-up. Researchers need to estimate losses from past experience and inflate the sample size. Calculate accordingly. These losses (particularly non-response, incomplete data, loss of follow-up) can be attributed to both areas of research (e.g., when studying sexuality and other sensitive issues, non-response rates can be high) and It has a lot to do with population. What researchers are trying to study. Therefore, researchers are advised to use non-response rates from previous studies in similar research areas and similar populations.
Any percentage of potential loss can be included to inflate the sample size, but there is no guarantee that the calculated sample size will be valid for a representative sample. In general, we recommend that a loss of less than 10% is an acceptable loss. However, there are differing opinions on the acceptable percentage of loss or wear and tear. [16] It depends on the type of research. At a minimum, it’s important to note that the greater the loss or wear and tear, the greater the compromise on the validity of the results.
Sample size calculation report
Sample size reports must be reproducible. This means that all parameters used should be reported. There are four parameters: confidence (mostly 95%), expected prevalence (mostly from the literature or pilot studies), accuracy or margin of error of the estimate (determined by the researcher), and expected loss ( researcher’s experience) is used. calculation. Also, the name of the software or calculator should be included with appropriate references. The Scalex SP calculator has a built-in draft his report that the user can copy and use. Make sure the report contains all the required parameters used.
[ad_2]
Source link

